Physically Based Rendering

Lights

Light is emitted by a light source, bounces around and eventually hits a camera. In general at each bounce light loses some of its intensity – accordingly light that hits the camera after fewer bounces is likely to be the most important. Therefore it makes sense to treat direct light sources differently than indirect light sources (because light bounces around a lot, basically everything is an indirect light source). Most rendering software distinguishes some specific types of light sources, the easiest of which is a point light. A point light is defined only by a position and an intensity of light. Previous chapters implicitly worked with point lights without explicitly mentioning them. An even easier type of light is the directional light, directly defined by an intensity and a direction. These lights simplify lighting calculations because light direction vectors do not need to be calculated based on the light’s position but are constant. Directional lights are used to simulate sun light – the sun is positioned so far away from earth that all light that hits the earth hits at almost the same angle.

More advanced rendering software supports area lights, which are a more appropriate approximation of real lights. Area lights can be simulated by placing lots of point lights or by modifying lighting calculations to use functions which approximate the forms of certain types of area lights. Most of today’s games do not yet support area lights.

BRDF

When a ray of light bounces of an opaque object, some of the light is reflected directly which is called specular reflection. Some of the light penetrates into material. Some part of that light is lost and some other part leaves the material again which is called diffuse reflection.

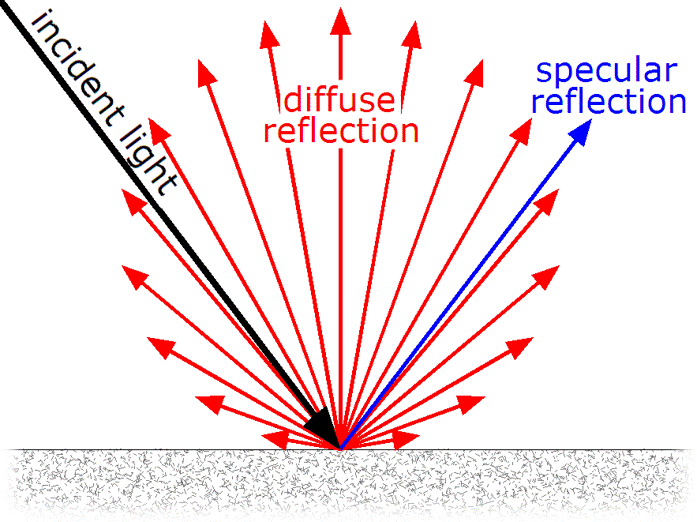
A function which tries to describe exactly what percentage of light is reflected at a given point is called a bidirectional reflectance distribution function. This BRDF works on a light vector and a camera vector and returns the ratio of reflected light.

A properly defined BRDF can be combined with a slow but very exact rendering algorithm like path tracing, which samples large amounts of random bounces at every rendered point, to create very realistic images. Most realtime rendering algorithms only directly calculate the first light bounces and some specific effects created by a second light bounce like hard shadows but a properly defined BRDF is just as important in realtime rendering algorithms. A very realistic BRDF however can highlight the shortcomings of the rendering algorithm. To offset this problem basic first bounce lighting calculations which calculate BRDFs just by using direct light sources to calculate the light vectors are increasingly combined with image based lighting – lighting information can be precalculated and put into cube maps. Sampling lighting information from cube maps can theoretically replace other lighting calculations but a cube map is only correct for a single point in space and precalculated cube maps cannot capture lighting information from dynamic objects. Cube maps are also prone to color range problems. A cube map side which directly captures a light source would have to contain much higher light values than other sides of the cube map– a problem well known from photography. These differences are generally too high to be captured properly in 32 bit pixel values.

BRDFs however also have shortcomings independent of the rendering algorithm. BRDFs cannot directly reproduce wavelength dependent reflection – a general problem that arises due to the representation of light as rgb-tuples. More importantly they cannot be used to calculate more complex diffuse reflections – light that penetrates a material generally does not leave the material at the same position. This is called subsurface scattering and missing out on calculating it becomes visible when the typical distance of light entry and light exit is larger than a pixel. Human skin is an often rendered material which has very apparent subsurface-scattering properties.

The standard BRDF definition assumes that the result is multiplied with the cosine of the angle between the light direction and the surface normal – aka the Phong diffuse term N⋅L. Based on this BRDFs can be checked against several rules to verify their physical plausibility. Common requirements for a physically plausible BRDF are:

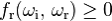
A BRDF should never return negative values.

When the light and camera vector are swapped, a BRDF should return the same value. This is in accordance to light ray calculations in physics like direct reflection or refraction.

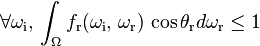
BRDFs are called energy conserving when they do not emit more light than they receive at any given point.

For all of that it is important to avoid calculating using gamma encoded color values. As monitors mostly work with a gamma value of 2.2 and images are saved using an inverted gamma value of 1 / 2.2 so they can be displayed properly on a monitor without further modifications, rendering algorithms can work in a linear color space by taking image color values to a power of 2.2 and taking calculated color values to a power of 1 / 2.2 before writing them to the framebuffer.

The Phong lighting model is a proper BRDF (at least when the ambient term is removed). Its diffuse term (L⋅N) is generally close enough to more physically accurate BRDFs that games tend to retain it. But that is not the case for the specular term.

A very visible property of reflection in real life that is completely ignored by the Phong lighting model is the Fresnel effect. The amount of light reflected directly from a material increases with the angle of incidence. This is especially apparent for water surfaces where reflections disappear when the surface is viewed from directly above. But the Fresnel effect is visible for every material.

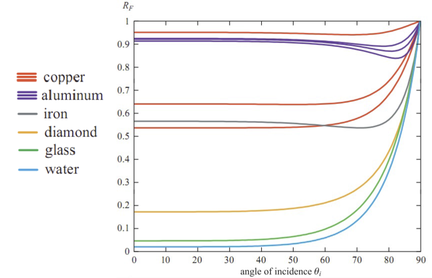
Realtime applications often use the Schlick approximation which calculates the Fresnel graph of a material based on the minimal reflection intensity value of a material:

Schlick(spec, light, normal) = spec + (1 - spec) (1 - (light⋅normal))^5

Microfacet Models

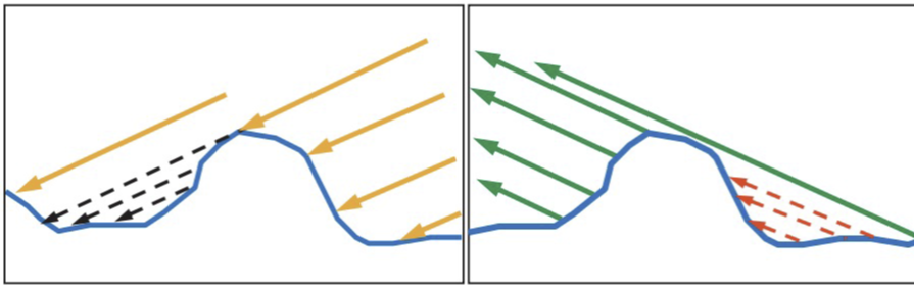
More physically correct BRDFs also consider the generally rough surfaces of materials. In reality almost no surface is actually flat when viewed at the small sizes relevant for light waves. Considering a mirror a direct reflection can only be seen at a specific point of the mirror when the surface normal evenly divides the angle between the light and the view vector i.e. when it equals the half vector. Accordingly the so called microfacet models, which consider any surface to be constructed of lots of tiny, flat facets only considers those facets for specular reflection which’s normals equal the halfvector.

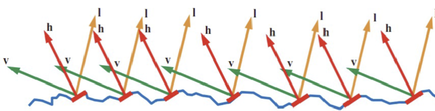
Microfacet based BRDFs generally have the form

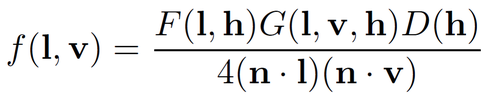
F(l, h) is the Fresnel factor - the Schlick approximation can be used here, but when used in a microfacet model it has to be calculated based on the halfvector instead of the surface normal.

D(h) is the normal distribution function which describes based on the surface normal and a roughness factor what portion of the microfacets has a normal that equals the halfvector. This is basically what the specular term of the Phong lighting model does but physically based models tend to use more involved models like the Trowbridge-Reitz (also called GGX) function:

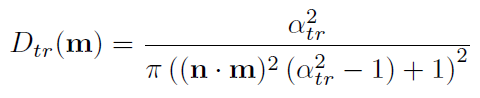
G(l, v, h) is the geometry factor which describes what portion of the light is not lost due to shadowing on the microfacet surface.

Some G functions cancel out the denominator of the general microfacet BRDF (4⋅(n⋅l)⋅(n⋅v)) – the combination of those terms is sometimes called the visibility function.

A reasonable G function is the Cook-Torrance function:

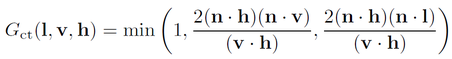
Physically Based Rendering

Physically based rendering in games generally means that images are rendered in a gamma correct way using a microfacet BRDF in combination with image based lighting. Material properties tend to be defined based on real world material properties which can be inspected using cameras and light polarization filters – specular reflections conserve light polarization while diffuse reflections randomize polarization. Photos of pure diffuse and specular reflection show that specular reflection is a big factor even for materials like cardboard. It also shows that metals have no diffuse reflections at all, any light that penetrates metal disappears. Also most modern engines can put all material properties in textures so that meshes are typically textured using a diffuse texture, a specular texture, a roughness texture and a normal map.

To add the image based lighting components games precalculate lots of cube maps which are placed manually in the level editor.

During runtime approximations are used to interpolate the cube maps and because cube maps cannot capture dynamic content a screen-space raytracing pass is added that works based on the depth buffer. All of this is a rough process that’s still refined in newer games.

Ambient Occlusion

Another seemingly simple lighting effect that is very apparent in the real world are small shadows produced by small surface bumps – like the tiny shadows in wrinkles of the skin. Calculating this effect properly in realtime is very difficult and games use an easy shortcut which is called Screen Space Ambient Occlusion. After rendering a post processing filter detects sharp differences in the final screen space normals and darkens the image at those positions. The look of modern games is very much defined by Screen Space Ambient Occlusion which also explains some typical image errors like dark shadows around characters which appear when they stand close to a wall.

Global Illumination

The big unsolved mystery of realtime graphics however is global illumination – properly calculating ambient light due to the many light bounces that typically happens before a light ray hits the camera.

Spherical Harmonics Lighting and Voxel Cone Tracing are two keywords for methods that are currently used or researched but most games still fall back to precalculated lighting to add an ambient component.